Word Problems on H.C.F. and L.C.M.
We have already learnt H.C.F, L.C.M and the relationship between the two and now we will learn on how to do word problems on H.C.F. and L.C.M.
Note: In word problems on H.C.F. and L.C.M we have to remember two points:
• When we are asked to find out maximum, highest or largest of anything we are required to do H.C.F as it is Highest Common factor.
• When we are asked to find out minimum, lowest or smallest of anything we are required to do L.C.M as it is Lowest Common Multiple
Here few examples are illustrated on word problem of H.C.F. and L.C.M
1. There are two pots each having a volume of 256 cu.cm and 264 cu.cm respectively. Find the maximum volume of same pot that should be made which will fit into both the pots.
Solution:
The maximum volume of pot that can be made to fit into both the pots are: H.C.F of 256 and 264
Factors of 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2^8
Factors of 264 = 2 × 2 × 2 × 3 = 2^3 × 3 × 11
H.C.F of 256 and 264 = 2^3 = 8
The greatest volume of the pot that can be fitted into both the pots = 8 cu. cm
Explanation:
The problem asks to find out the greatest size of pot that can fit into both the pots hence we need to find out the H.C.F of 256 and 264.
2. Find the greatest number that can divide 12 and 48 exactly without leaving any remainder.
Solution:
Greatest number = H.C.F of 12 and 48
Factors of 12 = 3× 2^2
Factors of 48 = 3 × 2^4
Therefore, H.C.F of 12 and 48 = 2^2 × 3 = 4 × 3 = 12
Greatest number = 12
Explanation:
This sum has also asked to find out the greatest number hence we need to do H.C.F of 12 and 48.
3. In a hostel room there are three girls. During winter vacation all the three girls left for their home and after coming back each of the girls decided to visit their home town after 2 months, 4 months and 6 months respectively. After how many months again three girls will together go to their home to spend their vacation?
Solution:
We have to find out the L.C.M of 2, 4 and 6
Factors of 2 = 2
Factors of 4 = 2 × 2
Factors of 6 = 2 × 3
L.C.M of 2, 4 and 6 = 2 × 2 × 3 = 12
The three girls will again go together after 12 months to spend their vacation in their hometown.
Explanation:
The sum has asked that after how months the three girls will again visit their hometown together if they go at an interval of 2, 4 and 6 months respectively. Hence, we need to carry out the L.C.M of 2, 4 and 6.
From Word Problems on H.C.F. and L.C.M. to HOME PAGE
Recent Articles
-
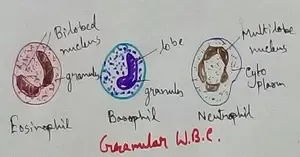
Formed Elements of Blood | Erythrocytes | ESR |Leukocytes |Neutrophils
Jan 15, 26 01:25 AM
Formed elements formed elements are constitute about 45 % of blood afeias haematocrit value packed cell volume mostly of red blood corpuscles and are of 3 types- erythrocytes, leukocytes and blood pla… -
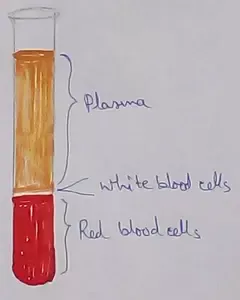
What Is Plasma? | Blood Plasma | Proteins | Nutrients | Cholesterol
Nov 07, 25 10:29 AM
Blood is a mobile fluid which is a connective tissue and is derived from the mesoderm like cell any other connective tissue. Colour of blood is reddish and that flows inside the blood vessels by means… -
Disorders of Respiratory System | Tuberculosis | Pleurisy | Emphysema
Oct 28, 25 11:39 PM
Tuberculosis is very common disease and is caused by a type of bacteria called Mycobacterium tuberculosis. This disease causes different trouble in the respiration and infection of several parts of th… -
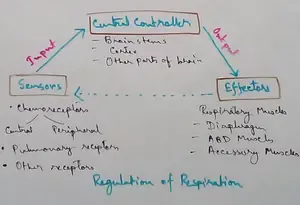
Regulation of Respiration | Respiratory Centres | Inspiratory Area |
Oct 14, 25 12:13 AM
Respiratory Centre is the area that controls the rate of respiration and it is observed to be located in medulla oblongata and pons. Respiratory Centre has the following will dispersed components like… -
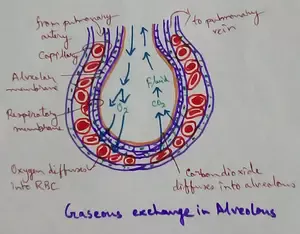
Explain Transport of Gases | External Respiration | Tissue Respiration
Oct 09, 25 11:35 PM
In humans gaseous exchange is completed in the following ways the steps are - External Respiration or Breathing - Breathing in false taking in of Oxygen and giving out of carbon dioxide in the body. M…

New! Comments
Have your say about what you just read! Leave me a comment in the box below.