Simplification of Numerical Expressions
This topic would discuss on simplification of numerical expression using BODMAS rule. The word BODMAS stands for:
B stands for Brackets
O stands for Of
D stands for Division
M stands for Multiplication
A stands for Addition
S stands for Subtraction
Now in brackets there are three sub categories:
( ) ……. First bracket
{ }……..Second bracket
[ ] ……...Third Bracket
In this bracket classification there is certain rule. The rule is that the operation in first bracket has to be performed first then the operation in second bracket and finally the operation in third bracket.
Here are few examples on Simplification of numerical expressions:
1. 12 + [2 { 13 ÷ (50 + 15)}]
Solution:
12 + [2 {13 ÷ (50 + 15)}]
= 12 + [2 {13 ÷ 65}] The first bracket is solved first
= 12 + [2 × 0.2] The operation of the second bracket is done
= 12 + 0.4
= 12.4
Explanation:
We can see that under first bracket 50 and 15 is first added to get 65. Hence the operation of the first bracket is over. Then 13 is divided by 65 to get 0.2 and hence we can say that the operation of the second bracket is done. Then 2 is multiplied with 0.2 to get 0.4 which involves completion of the operation of third bracket. Now finally 12 is added to 0.4 to get 12.4 which is the final answer.
2. 56 + 4 × 2 – ( 30 ÷ {18 – 3})
Solution:
56 + 4 × 2 – { 30 ÷ (18 – 3)}
= 56 + 4 × 2 – {30 ÷ 15} Operation of first bracket performed
= 56 + 4 × 2 – 2 Operation of second bracket performed
= 56 + 8 – 2
= 64 – 2
= 62
Explanation:
We can see in this problem that there are only two brackets first bracket and second bracket. Therefore, we have to perform the operation of the first bracket and then second bracket. Under the first bracket we have to first perform subtraction that is 3 subtracted from 18 we get 15. Then under second bracket 30 is divided by 15 to get 2. Then we have three more operations to perform that is addition, multiplication and subtraction. So according to BODMAS rule we have performed first multiplication then addition and lastly subtraction to get the final result as 62.
3. 15 + 5 × (115 × 0) + 20 – (15 ÷ 3)
Solution:
15 + 5 × (115 × 0) + 20 – (15 ÷ 3)
= 15 + 5 × 0 + 20 – 5 Operation of first bracket performed
= 15 + 20 – 5
= 35 – 5
= 30
Explanation:
Here in this sum we only have first bracket but there are two first brackets. These two first brackets have to be solved in same step only. After solving the operation in two first brackets we have to carry out the other operations like addition, multiplication, and subtraction. First multiplication is done then addition and lastly subtraction according to BODMAS rule.
From Simplification of Numerical Expressions to HOME PAGE
Recent Articles
-
Plants Around Us | Big & Small Plants | Shrubs & Herbs | Water Plants
Feb 03, 26 02:01 AM
We see different types of plants around us. Plants are living things. They breathe and grow. They also reproduce. Most of the plants grow on land. Some plants grow in water. -
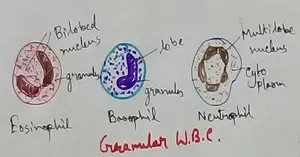
Formed Elements of Blood | Erythrocytes | ESR |Leukocytes |Neutrophils
Jan 15, 26 01:25 AM
Formed elements formed elements are constitute about 45 % of blood afeias haematocrit value packed cell volume mostly of red blood corpuscles and are of 3 types- erythrocytes, leukocytes and blood pla… -
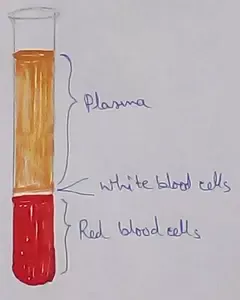
What Is Plasma? | Blood Plasma | Proteins | Nutrients | Cholesterol
Nov 07, 25 10:29 AM
Blood is a mobile fluid which is a connective tissue and is derived from the mesoderm like cell any other connective tissue. Colour of blood is reddish and that flows inside the blood vessels by means… -
Disorders of Respiratory System | Tuberculosis | Pleurisy | Emphysema
Oct 28, 25 11:39 PM
Tuberculosis is very common disease and is caused by a type of bacteria called Mycobacterium tuberculosis. This disease causes different trouble in the respiration and infection of several parts of th… -
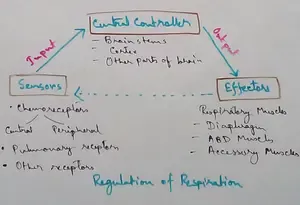
Regulation of Respiration | Respiratory Centres | Inspiratory Area |
Oct 14, 25 12:13 AM
Respiratory Centre is the area that controls the rate of respiration and it is observed to be located in medulla oblongata and pons. Respiratory Centre has the following will dispersed components like…



New! Comments
Have your say about what you just read! Leave me a comment in the box below.