Divisible by 8
The most common method to check whether a number is divisible by 8 is to divide and see if the quotient is a whole number or not? If the quotient is a whole number then the given number is divisible by 8. But there is an easier way to check by using the divisibility rule.
Divisibility Rule of 8: The divisibility rule of 8 states that if the number formed by taking the last three digits is divisible by 8 then the whole number is divisible by 8.
For Example: Check whether 5864 is divisible by 8 or not?
Since the last three digits are 864 and 864/8 = 108. Hence, the number 5864 is divisible by 8.
Here are few Examples on the Divisibility Rule of 8:
1. Check whether the following number are divisible by 8 or not?
(i) 7655
(ii)3248
(iii) 8880
(iv) 3697
(v)1154
(vi)7256
(vii) 4566
(viii)1008
(ix) 2726
(x) 9635
Solution:
(i) 7655
The last three digits = 655
Now 655 is not divisible by 8 as it gives = 81.875. Hence, 7655 is not divisible by 8
(ii)3248
The last three digits = 248
Now 248/8 = 31. Hence, 3248 is divisible by 8
(iii) 8880
880 is the last three digits
880/8 = 110. Hence 8880 is divisible by 8
iv) 3697
The last three digits = 697
Now 697 divided by 8 is 87.125. Hence, 3697 is not divisible by 8
v)1154
154 is formed by the last three digits
154/8 = 19.25 (which is not a whole number). Hence, 1154 is not divisible by 8
(vi)7256
The last three digits = 256
Now 256/8 = 32. Hence, 7256 is divisible by 8
(vii) 4566
The last three digits = 566
Now, 566 divided by 8 = 70.75 (not a whole number). Hence, 4566 is not divisible by 8
(viii)1008
008 is the last three digit
Now, 8/8 = 1. Hence, 1008 is divisible by 8
(ix) 2726
The last three digit = 726
Now, 726 divided by 8 = 90.75. Hence, 2726 is not divisible by 8
(x) 9635
The last three digits = 635
635 divided by 8 is 79.375
As, 635 is not divisible by 8 so, 9635 is also not divisible by 8
2. Rewrite the series with the numbers that are divisible by 8 with a different color:
8484 4295 6264 1020 3024 7728 5656 7432 5040 5689 4433 1223
Solution:
8484 4295 6264 1020 7432 5040 5689 3024 4433 5656 1223 7728
3. Fill in the blanks with digits o as to make the following number divisible by 8:
(i) 32 … 8
(ii) 10 … 2
(iii) 2 … 48
(iv) 564 …
(v) 410 …
(vi) 874 …
(vii) 30…6
(viii) 4 …16
Solution:
(i) 3288
(ii) 1032
(iii) 2848
(iv) 5640
(v) 4104
vi) 8744
(vii) 3016
(viii) 4816
Note: In the above example we have to put such digits so that the number formed by the last three digit is divisible by 8.
From Divisible by 8 to HOME PAGE
Recent Articles
-
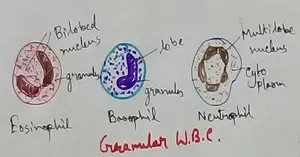
Formed Elements of Blood | Erythrocytes | ESR |Leukocytes |Neutrophils
Jan 15, 26 01:25 AM
Formed elements formed elements are constitute about 45 % of blood afeias haematocrit value packed cell volume mostly of red blood corpuscles and are of 3 types- erythrocytes, leukocytes and blood pla… -
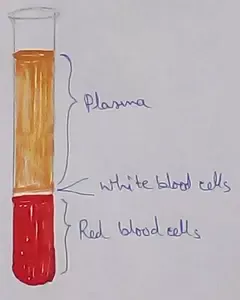
What Is Plasma? | Blood Plasma | Proteins | Nutrients | Cholesterol
Nov 07, 25 10:29 AM
Blood is a mobile fluid which is a connective tissue and is derived from the mesoderm like cell any other connective tissue. Colour of blood is reddish and that flows inside the blood vessels by means… -
Disorders of Respiratory System | Tuberculosis | Pleurisy | Emphysema
Oct 28, 25 11:39 PM
Tuberculosis is very common disease and is caused by a type of bacteria called Mycobacterium tuberculosis. This disease causes different trouble in the respiration and infection of several parts of th… -
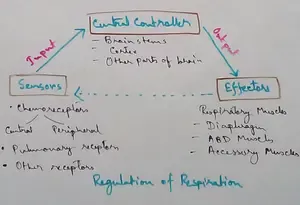
Regulation of Respiration | Respiratory Centres | Inspiratory Area |
Oct 14, 25 12:13 AM
Respiratory Centre is the area that controls the rate of respiration and it is observed to be located in medulla oblongata and pons. Respiratory Centre has the following will dispersed components like… -
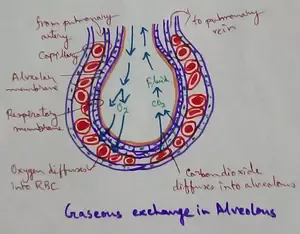
Explain Transport of Gases | External Respiration | Tissue Respiration
Oct 09, 25 11:35 PM
In humans gaseous exchange is completed in the following ways the steps are - External Respiration or Breathing - Breathing in false taking in of Oxygen and giving out of carbon dioxide in the body. M…


New! Comments
Have your say about what you just read! Leave me a comment in the box below.