Relationship between H.C.F. and L.C.M.
This topic discusses about the relationship between H.C.F and L.C.M in case of two numbers. The relationship between H.C.F and L.C. M of two number states that:
H.C.F × L.C.M = First Number × Second Number
Hence from this relationship we can find the following:
\[\textrm{H.C.F} = \frac{\textrm{First Number} \times \textrm{Second Number}}{\textrm{L.C.M.}}\]
\[\textrm{L.C.M.} = \frac{\textrm{First Number} \times \textrm{Second Number}}{\textrm{H.C.F.}}\]
\[\textrm{First Number} = \frac{\textrm{H.C.F.} \times \textrm{L.C.M.}}{\textrm{Second Number}}\]
\[\textrm{Second Number} = \frac{\textrm{H.C.F.} \times \textrm{L.C.M.}}{\textrm{First Number}}\]
To Justify this Relation here is an Example:
1. Suppose the two given numbers are 24 and 16. Justify the relationship between H.C.F and L.C.M
Solution:
The H. C.F of 24 and 18 by finding factors is:
The factors of 24 = 2 × 2 × 2 × 3 = 2^3×3
The factors of 18 = 2 × 3 × 3 = 3^2×2
The common prime factors of 24 and 18 = 2 and 3
The lowest power of 2 is 2
The lowest power of 3 is 3
Therefore, the Highest common factor (H.C.F) = 2 × 3 = 6
The L.C. M of 24 and 18 by prime factorization method:
The factors of 24 = 2 × 2 × 2 × 3 = 23 × 3
The factors of 18 = 2 × 3 × 3 = 32 × 2
The highest power of 2 = 23
The highest power of 3 = 32
Therefore, the lowest common multiple of 18 and 24 is 23 × 32 = 72
Now the product of H.C.F and L.C.M is 6 × 72 = 432
The product of 18 and 24 is 432
Hence, H.C.F × L.C.M = Product of two numbers
432 = 432 (verified)
Here are few more examples to illustrate relationship between H.C.F and L.C.M
2. The H.C.F of two numbers is 18 and their product is 94734. Find their L.C.M
Solution:
Given,
The highest common factor (H.C.F) of two numbers = 18
The product of two numbers = 94734
According to the relationship, we know,
H.C.F × L.C.M = First number × Second number
Or, H.C.F × L.C.M = product of the numbers
⟹ 18 × L.C.M = 94734
⟹ L.C.M = \(\frac{94734}{18}\)
⟹ L.C.M = 5263
Therefore, the lowest common multiple (L.C.M) of the two numbers = 5263
Explanation:
The H.C.F of two numbers is given and their product is given. By applying the relation we need to find out the L.C.M
3. The L.C.M and H.C.F of two numbers are 144 and 36 respectively. If one number is 54, then find the other number.
Solution:
Given,
The highest common factor (H.C.F) of two numbers = 36
The lowest common multiple (L.C.M) of two numbers = 144
One of the two numbers is 54
According to the relationship, we know,
H.C.F × L.C.M = First number × Second number
⟹ 36 × 144 = 54 × Second number
⟹ 5184 = 54 × Second number
⟹ Second Number = \(\frac{5184}{54}\)
⟹ Second Number = 96
Therefore, the other number is 96
Explanation:
The H.C.F and L.C.M of two numbers is given and one of the numbers is given. By applying the relationship we can find out the other/ second number.
From Relationship between H.C.F. and L.C.M. to HOME PAGE
Recent Articles
-
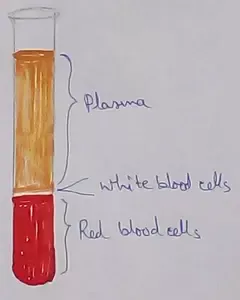
What Is Plasma? | Blood Plasma | Proteins | Nutrients | Cholesterol
Nov 07, 25 10:29 AM
Blood is a mobile fluid which is a connective tissue and is derived from the mesoderm like cell any other connective tissue. Colour of blood is reddish and that flows inside the blood vessels by means… -
Disorders of Respiratory System | Tuberculosis | Pleurisy | Emphysema
Oct 28, 25 11:39 PM
Tuberculosis is very common disease and is caused by a type of bacteria called Mycobacterium tuberculosis. This disease causes different trouble in the respiration and infection of several parts of th… -
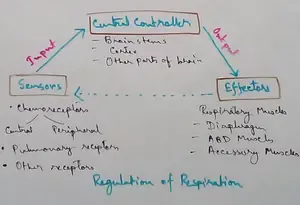
Regulation of Respiration | Respiratory Centres | Inspiratory Area |
Oct 14, 25 12:13 AM
Respiratory Centre is the area that controls the rate of respiration and it is observed to be located in medulla oblongata and pons. Respiratory Centre has the following will dispersed components like… -
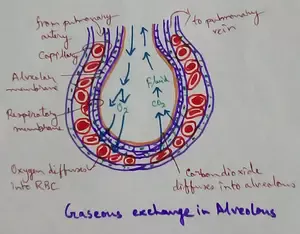
Explain Transport of Gases | External Respiration | Tissue Respiration
Oct 09, 25 11:35 PM
In humans gaseous exchange is completed in the following ways the steps are - External Respiration or Breathing - Breathing in false taking in of Oxygen and giving out of carbon dioxide in the body. M… -
Kind and Number of Teeth | Location of Teeth in Mouth | Care of Teeth
Sep 11, 25 12:52 AM
Kind and Number of Teeth



New! Comments
Have your say about what you just read! Leave me a comment in the box below.