Simplification of Fractions
Still now we have learnt about addition, subtraction, multiplication and division of fractions separately and have also discussed about the properties of each of them separately. However, now we move onto simplification of fraction. What does it mean?
The basic four operations that is addition, subtraction, multiplication or division are present in a single sum and hence we will have to carry out all the four operations together one by one. For doing so we have to remember ‘BODMAS’
What does ‘BODMAS’ stands for?
B = Brackets
O = Of
D = Division
M= Multiplication
A = Addition
S = Subtraction
We will carry out the task of simplification in this order.
However, there are three types of brackets:
()= first bracket
{} = second bracket
[]= third bracket
The rule is that anything in the bracket should be simplified first and in accordance with the brackets. The operation of first bracket should be done first then followed by second and third bracket.
Here are few examples showing simplification of fractions:
1. (21/3 + 52/3) × (6/7 ÷ 12/14)
= (7/3 + 17/3) × (6/7 × 14/12)
= ((7+17)/3) × ((6 ×14)/(7 ×12))
= 24/3 × 84/84
= 8 × 1
= 8
Explanation:
Here in this sum the operations in the brackets are carried out first according to the rule of ‘BODMAS’. Hence the addition and division in the first bracket have been carried out first and then both the answers of addition and division is multiplied. The answer from division is 1. And we know according to the properties of multiplication that if any fraction/ number is multiplied by 1 then the result is the fraction/ number itself.
80 – 17/2 × 2 + 13 ÷ 13/7
= 80 – 17/2 × 2+ 13 ÷ 13/7
= 80 – 17/2 × 2 + 13 × 7/13
= 80 – 17/2 × 2 + 7
= 80 – 17 + 7
= 80 + 7 – 17
=87 – 17
= 70
Explanation:
The sum is done following the rule of ‘BODMAS’. Four basic operations that is addition, subtraction, multiplication and division all are involved in this sum. According to ‘BODMAS’
First division is carried out then multiplication and then followed by subtraction and addition.
If we do not follow this sequence and carry out the operation according to the sequence in which the sum is given then we will get the answer wrong.
3. 12 7/8 + 6 2/3 × 24/16
= 103/8 + 20/3 × 24/16
= 103/8 + (20 ×24)/(3 ×16)
= 103/8 + 480/48
= (103 ×6+480 ×1)/48
= 1098/48
= (1098 ÷6)/(48 ÷6)
= 183/8
= 22 7/8
Explanation:
The sum is done following the rule of ‘BODMAS’. The basic operation that is addition and multiplication is involved in this sum. According to ‘BODMAS’ rule first multiplication is done and then addition is carried out. After multiplying the answer is first expressed in lowest terms and then into mixed fraction as it was an improper fraction.
From Simplification of Fractions to HOME PAGE
Recent Articles
-
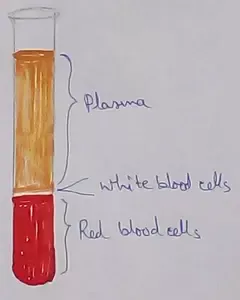
What Is Plasma? | Blood Plasma | Proteins | Nutrients | Cholesterol
Nov 07, 25 10:29 AM
Blood is a mobile fluid which is a connective tissue and is derived from the mesoderm like cell any other connective tissue. Colour of blood is reddish and that flows inside the blood vessels by means… -
Disorders of Respiratory System | Tuberculosis | Pleurisy | Emphysema
Oct 28, 25 11:39 PM
Tuberculosis is very common disease and is caused by a type of bacteria called Mycobacterium tuberculosis. This disease causes different trouble in the respiration and infection of several parts of th… -
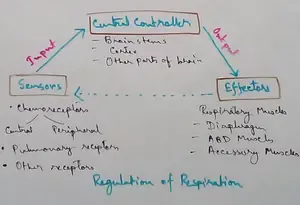
Regulation of Respiration | Respiratory Centres | Inspiratory Area |
Oct 14, 25 12:13 AM
Respiratory Centre is the area that controls the rate of respiration and it is observed to be located in medulla oblongata and pons. Respiratory Centre has the following will dispersed components like… -
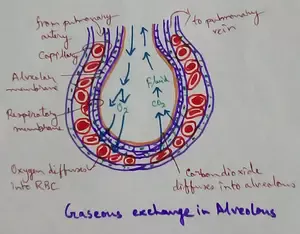
Explain Transport of Gases | External Respiration | Tissue Respiration
Oct 09, 25 11:35 PM
In humans gaseous exchange is completed in the following ways the steps are - External Respiration or Breathing - Breathing in false taking in of Oxygen and giving out of carbon dioxide in the body. M… -
Kind and Number of Teeth | Location of Teeth in Mouth | Care of Teeth
Sep 11, 25 12:52 AM
Kind and Number of Teeth



New! Comments
Have your say about what you just read! Leave me a comment in the box below.