Various Types of Numbers
Numbers are mathematical symbols or signs that help us to measure, count, and estimate. It is a real pride for we Indians that the most used system of numeration that is the Hindu Arabic system of numeration was invented by two Indian mathematician. Aryabhat in 5th century B.C and Brahmagupta in the 6th century B.C. the four basic operation using numbers are addition, subtraction, multiplication, division.
There are various types of numbers and we need to know what those types are.
Example: \(\frac{10}{8}\), …. ,0.2568, 0.98, ….., 8, 9, 10, …… are all numbers but of different types.
The different types of numbers are:
Natural Numbers: - A natural number is a positive integer, starting from 1. They are 1, 2, 3, 4, 5, 6, 7,…….etc. Natural numbers are also called counting numbers.
Integers: – An integer is a natural number, negative natural number including 0.
Example: -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 ,6, 7, 8…….etc.
Whole Numbers: – Whole are the basic counting numbers starting from 0.
They are 0, 1, 2, 3, 4, …….etc.
Real numbers: – Any number that is written in decimal form are called real numbers.
Example: 0.255689, 0.325, -0.258, …….etc. all real numbers can be represented on a number line.
Rational numbers: – Any number in p/q form is represented as rational number. p and q are natural numbers. The numerator of rational number can be zero but the denominator can never be zero.
Example: 25/2, 9/4
Irrational numbers: – Numbers which cannot be expressed in p/q form are termed as irrational numbers. These numbers are represented in decimals and the decimal numbers are repeated without repetition of the pattern of numerals.
Example: √3, √5….. etc
Few
other types of numbers are:
Even numbers: – Any whole number that is divisible by 2 that is without leaving any remainder is termed as prime number.
Example: 8, 10, 12, 14,….etc.
Otherwise we can say that the multiples of 2 are called even numbers. The difference between two even numbers is 2.
Odd numbers: – Any number that is not divisible by 2 (that is it leaves a remainder 1) are called odd numbers.
Example: 1, 3, 5, 7, 9, 11, 13, 15,……. etc.
One similarity between even and odd numbers is that the difference between any two odd numbers is also two.
Prime Numbers: - Numbers that are divisible by one and itself are prime numbers. that is these numbers have two factors 1 and itself. These numbers do not appear in the tables of any other number except one and itself.
Example: 2, 3, 5, 7, 11, ………..etc.
Composite Numbers: – Numbers that are divisible by other than one and itself are called composite numbers. These numbers have other factors except one and itself.
Example: 2, 4, 2156, 86, 84, 63,………etc
Twin Prime Numbers: – Any two prime numbers that have difference two are termed as twin prime numbers
Example: 41 and 43, 3 and 5, 29 and 31,.etc
Co- prime Numbers: – Any two number whose H.C.F is one is termed as co- prime or numbers that have a common factor as 1
Example: 15 and 17, 23 and 26
Problems on Various Types of Numbers:
1. Write all the EVEN numbers from 1 to 80
Solution:
Even numbers are numbers that are divisible by 2 or can be said multiples of 2.
If we write down the tables of 2 then all are prime number
2 × 1 =2
2 × 2 = 4
2 × 3 =6
2 × 4 = 8
2 × 5 = 10
2× 6 = 12
Like this it will go on and all are multiples of 2. More the difference between two even number is 2
Therefore, the even numbers from 1 to 80 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80
We can see that all are multiples of 2 and has a difference of 2
2. Write all the ODD numbers from 100 to 150
Solution:
Odd numbers are not divisible by 2 and do not appear in tables of 2.
Odd numbers do not end with 0, 2, 4, 6, and 8
Therefore, the odd numbers from 100 to 150 that do not end with 0, 2, 4, 6, 8 are 101, 103, 105, 107, 109, 111, 113, 115, 117, 119, 121, 123, 125, 127, 129, 131, 133, 135, 137, 139, 141, 143, 145, 147, 149
From Various Types of Numbers to HOME PAGE
Recent Articles
-
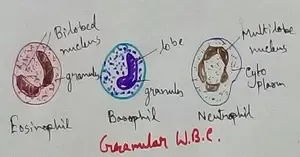
Formed Elements of Blood | Erythrocytes | ESR |Leukocytes |Neutrophils
Jan 15, 26 01:25 AM
Formed elements formed elements are constitute about 45 % of blood afeias haematocrit value packed cell volume mostly of red blood corpuscles and are of 3 types- erythrocytes, leukocytes and blood pla… -
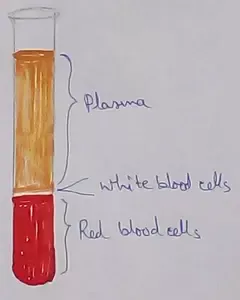
What Is Plasma? | Blood Plasma | Proteins | Nutrients | Cholesterol
Nov 07, 25 10:29 AM
Blood is a mobile fluid which is a connective tissue and is derived from the mesoderm like cell any other connective tissue. Colour of blood is reddish and that flows inside the blood vessels by means… -
Disorders of Respiratory System | Tuberculosis | Pleurisy | Emphysema
Oct 28, 25 11:39 PM
Tuberculosis is very common disease and is caused by a type of bacteria called Mycobacterium tuberculosis. This disease causes different trouble in the respiration and infection of several parts of th… -
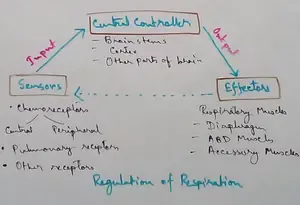
Regulation of Respiration | Respiratory Centres | Inspiratory Area |
Oct 14, 25 12:13 AM
Respiratory Centre is the area that controls the rate of respiration and it is observed to be located in medulla oblongata and pons. Respiratory Centre has the following will dispersed components like… -
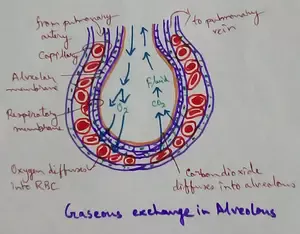
Explain Transport of Gases | External Respiration | Tissue Respiration
Oct 09, 25 11:35 PM
In humans gaseous exchange is completed in the following ways the steps are - External Respiration or Breathing - Breathing in false taking in of Oxygen and giving out of carbon dioxide in the body. M…



New! Comments
Have your say about what you just read! Leave me a comment in the box below.